Die Vorhersage oder die Berechnung eines resultierenden Alkoholgehaltes im Bier nehmen uns heutzutage installierte Rezepturprogramme oder frei verfügbare Tools im Internet ab.
Die Anwendungslogik dieser Tools implementiert dazu Lösungsansätze, die sich aus dem gesamten Portfolio der Brauermathematik bedienen - vom Dreisatz über Balling[Q002] bis hin zum höhergradigen Polynom.
Dem gegenüber steht die wohl bekannteste Faustformel in diesem Umfeld, die besagt, dass sich ca. ein Drittel der ursprünglichen Stammwürze in Alkohol umwandelt.
Was wäre, wenn man aus der Komplexität des Einen und der Einfachheit des Anderen einen Faktor ersinnt, der aus leicht verfügbaren Ist-Werten zuverlässig eine resultierende Alkoholkonzentration in ABV(Alcohol by volumne, Vol.-%, %v/v) ermittelt?
Natürlich ist der Autor des Artikels nicht der Erste, der sich des Themas annimmt. Im Internet finden sich unzählige Lösungen zur Planung oder zur Berechnung von resultierenden Alkoholgehalten im Bier.
Offensichtlich ist man auf internationaler Bühne besonders fleißig, was schon alleine dadurch deutlich wird, welche Einheiten zur Verrechnung verwendet werden. Mit zunehmender Präzision und Richtigkeit werden die verfügbaren Lösungen allerdings immer komplexer, sodass von einem einfachen Faktor eigentlich keine Rede mehr sein kann.
Am Ende des Artikels befindet sich eine Zusammenfassung der recherchierten Onlineressourcen mit dem Titel ABV via Faktor im Internet. Unbedingt 'mal 'reinlesen. Da sind ganz tolle Sachen mit dabei.
Die Inspiration für einen neuen Faktor
Inspiriert durch den Brauweltartikel "Vergärungsziffer zur Quantifizierung der Drinkability "[Q001] bot sich die Gelegenheit, das Thema ganz neu aufzubereiten. Hier die entscheidende Passage im benannten Artikel in einer Zusammenfassung:
Laut Balling entsteht aus 2,0665 g Extrakt 1 g Alkohol(Ethanol).
Die Dichte von Ethanol bei 20 °C ist 0,789 g/ml. Über die Dichte von Ethanol berechnet nimmt 1 g Ethanol bei 20 °C ein Volumen von 1 / 0,789 = 1,27 ml ein.
Mittels der 2,0665 g Extrakt, die Balling für die Entstehung von 1 g Alkohol gefunden hat und mit dem Volumen das 1 g Alkohol einnimmt, lässt sich ein theoretisch maximales Verhältnis von vergärbarer Extraktmenge zum resultierenden Alkoholgehalt in Vol.-%(ABV) berechnen:2,0665 / 1,27 = 1,63
Zugegebenermaßen liest sich die Formulierung "ein theoretisch maximales Verhältnis von vergärbarer Extraktmenge zum resultierenden Alkoholgehalt in Vol.-%" etwas sperrig. Einfacher ausgedrückt lässt sich über den Faktor 1,63 eine vergärbare Extraktmenge in g/100g wässriger Lösung direkt in eine Alkoholkonzentration in Vol.-%(ABV) umrechnen.
Formel 01: Berechnung ABV aus einer vergärbaren Extraktmenge [g/100g]
ABV = vergärbare Extraktmenge [g/100g] / 1,63
Da trifft es sich ganz gut, dass sich die Stammwürze in °P über Massen- bzw. Gewichtsprozente definiert. Nimmt man für einen kurzen Moment an, dass eine Bierwürze zu 100 % vergärbar ist, dann ließe sich ein resultierender Alkoholgehalt in Vol.-%(ABV) nach diesem Muster direkt aus der Stammwürze P berechnen:
Formel 02: Berechnung ABV aus Grad Plato °P für den Fall, dass P zu 100 % vergärbar ist
ABV = P / 1,63
Beispiel 01: Berechnung ABV aus einer Würze mit 12 °P, die zu 100 % vergärbar ist
ABV = 12,0 / 1,63 = 7,36 Vol.-%
Eine Bierwürze mit 12,0 °P, die zu 100 % vergärbar ist(wirklich), wird im fertigen Bier einen Alkoholgehalt von 7,36 Vol.-% erzeugen(theoretisch maximal).
Der interessante Aspekt ist der, dass der Faktor für alle Fermentationen gelten darf, sofern es sich bei der Extraktmenge um eine wirklich vergärbare Extraktmenge handelt und mit Fermentation eine "alkoholische Gärung" gemeint ist. Aus welcher Extraktquelle(Fermentables) die Extraktmenge stammt, wie sie gewonnen wurde(Maischen), wann sie zum Einsatz kam(Speise/Zucker) oder durch wen diese Extraktmenge vergoren wurde(Hefestamm) - das ist für einen über den Faktor 1,63 berechneten Alkoholgehalt gänzlich irrelevant.
Ein bekannter Anwendungsfall macht das deutlich:
In Hobbybrauerkreisen ist eine Dosage von Haushaltszucker(Saccharose) zum Zwecke einer Karbonisierung nicht unüblich. Dem schließt sich oft die Frage an, um wie viel Vol.-% sich der Alkoholgehalt durch eine Zuckerdosage im Bier erhöht. Lässt man die Dichte von Bier außen vor und nimmt an, dass 1 L endvergorenes Bier einer Masse von ca. 1000 g entspricht, dann darf für Speisegaben mit Haushaltszucker folgender allgemeiner Ansatz gelten:
Formel 03: Berechnung ABV aus einer Haushaltszuckerdosage [g/L Bier]
ABV = Haushaltszuckerdosage [g/L Bier] / 16,3
Beispiel 02: Zunahme ABV durch eine Haushaltszuckerdosage von 8 g/L Bier
ABV = 8 [g/L] / 16,3 = 0,49 Vol.-%
Durch die Dosage von 8 [g/L] Haushaltszucker nimmt der Alkoholgehalt im Bier um ca. 0,5 Vol.-% zu. Voraussetzung ist, dass der eingesetzte Hefestamm den Haushaltszucker zu 100 % vergären kann, wovon man im Umfeld einer gewollten Karbonisierung ausgehen kann.
Die Idee zur Entwicklung eines neuen Faktors
Der Faktor 1,63, angewendet auf eine vergärbare Extraktmenge, darf als gesichert gelten [Q001-Q003].
Die Stammwürze P beschreibt aber keine vergärbare Extraktmenge, sondern vielmehr eine Extraktkonzentration in [g/100 g] unmittelbar vor der Vergärung.
Gelingt es, denjenigen Teil der Stammwürze bzw. der Extraktmenge zu berechnen der vergärbar ist, darf der Faktor 1,63 auf diese berechnete Extraktmenge angewendet werden.
Für den Brauer ist die Berechnung einer vergärbaren Extraktmenge oder einer bereits vergorenen Extraktmenge keine grosse Sache, geht er doch schon im Rezepturumfeld und während der Herstellung beinahe täglich damit um. Sie folgt dem immer gleichen Muster:
Extraktgehalt vor der Gärung - Extraktgehalt während/nach der Gärung
Der Extraktgehalt vor der Gärung entspricht der Stammwürze P und der Extraktgehalt während/nach der Gärung entspricht dem Extrakt scheinbar Es[%mas].
Mit den Angaben zu P und Es lässt sich eine scheinbar vergorene Extraktmenge bzw. eine scheinbar vergärbare Extraktmenge vEs[%mas] berechnen:
Formel 04: Berechnung einer scheinbar vergorenen/vergärbaren Extraktmenge vEs [%mas] aus °P [%mas] und Es [%mas]
vEs = P - Es
Beispiel 03: Berechnung einer scheinbar vergorenenen Extraktmenge vEs aus P und Es
P [%mas] = 12,0
Es [%mas] = 2,4
vEs [%mas] = 12,0 % - 2,4 % = 9,6 %
In Worte gefasst: scheinbar wurden 9,6 °P der ursprünglichen Stammwürze von 12 °P vergoren.
Die Formel 02 kann jetzt so abgeändert werden, dass sie anstatt mit der Stammwürze °P mit der scheinbar vergärbaren Extraktmenge vEs [%mas] rechnet:
Formel 05: Berechnung ABV aus einer scheinbar vergärbaren Extraktmenge vEs [%mas]
ABV = vEs[P-Es] / 1,63
Beispiel 04: Berechnung ABV aus einer Würze mit 12 °P, die scheinbar zu 80 % vergärbar ist(Es = 2,4%)
ABV = (12,0 % - 2,4 %) / 1,63 = 9,6 % / 1,63 = 5,89 Vol.-%
Für die Eckdaten aus dem Beispiel 04 (P = 12,0 %, Es = 2,4 %, Vs = 80 %) müsste sich nach Balling, und unter Berücksichtigung der Dichtewerte für Bier und Ethanol, ein Alkoholgehalt von 5,07 Vol.-% ergeben.
Für das gewählte Beispiel und im Abgleich mit der Ballingformel ist die Ergebnislage für den ABV via Faktor berechnet etwas unerfreulich - aber der Weg scheint der richtige.
Balling selbst ist es, der schon 1845 in Band 1 [Q002], Seite 189, einen entscheidenden Hinweis für mögliche Abweichungen gibt. Zitat 01:
Der Verlust an der Dichte der gährenden Flüssigkeit während ihres Gährungsverlaufes hat zwei sich bedingende Ursachen, nämlich einmal: das Verschwinden des Zuckers aus derselben durch sein zerfallen in Alkohol und Kohlensäure, und zweitens: die Bildung von Alkohol, eines Körpers, welcher spezifisch leichter ist als Wasser.
Vor allem Letzteres ist umgangssprachlich als "Alkoholfehler" bekannt und sorgt regelmäßig für Mißverständnisse in der Kommunikation von festgestellten Extraktwerten oder daraus berechneten Vergärungsgraden. Hier beginnt aber auch, weshalb wir bis Heute in der Analytik und im Sprachgebrauch zwischen scheinbar und wirklich für Extraktangaben und Vergärungsgrade unterscheiden.
- Extrakt scheinbar Es[%mas]
- Extrakt wirklich Ew[%mas]
- Vergärungsgrad scheinbar Vs[%]
- Vergärungsgrad wirklich Vw[%]
Nach Balling besteht zwischen wirklichen und scheinbaren Extraktwerten und Vergärungsgraden eine nahezu lineare Beziehung, die Balling als Attenuationsquotient beschreibt. Er schreibt dazu, Zitat 02 (Band 1 [Q002], Seite 203):
Dieser Attennuationsquotient zeigt daher an, um wie vielmal die scheinbare Attenuation größer ist als die wirkliche.
Heute ist dieser Attennuationsquotient als "Ballingfaktor" oder als "Balling'scher Attenuationsfaktor" bekannt. Balling hat den Faktor bestimmt und einen Wert von 0,81 ermittelt. Für Berechnungen wird der Ballingfaktor meist noch etwas exakter angegeben [Q004]:
Ballingfaktor = 0,8192
In Beispiel 04(Formel 05) wurde der Faktor 1,63 auf die scheinbar vergärbare Extraktmenge vEs [%mas] angewendet - mit mäßigem Erfolg. Mit dem Ballingfaktor lässt sich die scheinbar vergärbare Extraktmenge vEs [%mas] in eine wirklich vergärbare Extraktmenge vEw [%mas] umrechnen. Damit wäre die Forderung von oben erfüllt:
Gelingt es, denjenigen Teil der Stammwürze bzw. der Extraktmenge zu berechnen der vergärbar ist, darf der Faktor 1,63 auf diese berechnete Extraktmenge angewendet werden
Formel 06: Umrechnung vEs [%mas] in vEw [%mas] via Ballingfaktor
vEw [%mas] = vEs [%mas] x 0,8192
Beispiel 05: Berechnung einer wirklich vergorenenen Extraktmenge vEw aus P und Es
P [%mas] = 12,0
Es [%mas] = 2,4 ( Vs = 80 %)
vEs [%mas] = 12,0 % - 2,4 % = 9,6 %
vEw [%mas] = 9,6 % x 0,8192 = 7,9 %
In Worte gefasst: Von einer Würze mit 12 °P und mit einem scheinbaren Vergärungsgrad Vs von 80 % wurden 7,9 °P (wirklich) vergorgen.
Beispiel 06: Berechnung ABV aus einer wirklich vergorenenen Extraktmenge vEw = 7,9 % (Eckdaten siehe Beispiel 05)
ABV = 7,9 / 1,63 = 4,85 Vol.-%
Im Beispiel 04 wurde für die selben Eckdaten eine Alkoholkonzentration von 5,89 Vol.-% berechnet. Korrigiert durch den Ballingfaktor für die vergärbare Extraktmenge jetzt neu zu 4,85 Vol.-%. Die Abweichung zum wahren Wert (5,07 Vol.-%) ist für das konstruierte Beispiel sehr viel besser geworden, allerdings bleibt die Abweichung bis hier hin unerklärt und das nur für diesen Einzelfall.
Es stand zu erwarten, dass ein weiterer Feinschliff die Ergebnislage nur noch geringfügig verbessert, aber sich gleichzeitig das zugehörige Formelwerk mehr und mehr aufbläht und der ursprüngliche Ansatz eines einfachen Faktors dabei verloren geht. Den bisherigen Lösungsansatz mit der Formel 07 abzuschliessen war die Konsequenz:
Formel 07: Berechnung ABV aus P, Es, Ballingfaktor 0,8192 und Alkoholfaktor 1,63
ABV = (P - Es) x 0,8192 / 1,63
Ein neuer Ansatz muss her
Sowohl der Alkoholfaktor 1,63 als auch der Attenuationsfaktor(Ballingfaktor) 0,8192 entstammt einer Lehre - der von Balling[Q001-Q002].
Schade nur, dass sie nichts voneinander wissen. Zeit sie, im Sinne von Vereinfachung, miteinander bekannt zu machen.
Die Formel 07 lässt sich durch Umformung auch so darstellen:
ABV = (P - Es) / (1,63 / 0,8192)
Im Nenner der Formel ergibt sich, gebildet aus Alkoholfaktor 1,63 und Ballingfaktor 0,8192, ein neuer Quotient zu:
1,63 / 0,8192 = 1,98975
In Entsprechung lässt sich die Formel 07 vereinfachen:
Formel 08: Berechnung ABV aus P, Es und Faktor F = 1,99
ABV = (P - Es) / F
Von Rundungsfehlern abgesehen liefert die Formel 08 ein identisches Ergebnis zur Formel 07 (4,85 Vol.-%)
Ähnlich falsch, aber immerhin war eine Vereinfachung gefunden, die die Ermittlung eines Faktors wesentlich vereinfacht.
Die bislang gewählten Beispiele für P, Es, Vs und ABV waren nicht ganz unbewusst gewählt. Zumindest für diesen einen Beispielfall sollten die bekannten Größen als Orientierung für die Neuausrichtung des Faktors dienen. Dazu wird die Formel 08 nach dem Faktor F umgestellt und die bekannten Größen werden in die Formel eingesetzt.
Formel 09: Berechnung Alkoholfaktor aus P, Es und ABV
F = (P - Es) / ABV
Beispiel 07: Rückrechnung eines Alkoholfaktors aus bekannten Größen
P [%mas] = 12,0
Es [%mas] = 2,4 (Vs = 80 %)
ABV [Vol.-%] = 5,07 %
F = (12,0 - 2,4) / 5,07 = 1,89
Die Faktoren F (1,89 Probe / 1,99 Theorie) liegen nicht weit auseinander, aber nur auf den ersten Blick und nur für das gewählte Beispiel.
Grob gefasst liegt die Wahrheit für einen einfachen ABV-Faktor nicht bei 1,63, sondern eher zwischen 1,80 und 2,00.
Für die Weiterentwicklung des Faktors war es wichtig zu wissen, wo die Grenzen für eine derartige Vereinfachung liegen und entsprechend galt es Gültigkeitsbereiche festzulegen.
Ziele des Faktors
- Keine komplizieren Rechenwege, einfache Handhabung und leicht verständlich
- Der Faktor soll mit Größen rechnen, die auch ein Kleinbrauer ermitteln kann oder ohnehin schon verfügbar hat (Spindelwerte für P und Es)
- Keine zusätzlichen Umrechnungen (Dichte, Extrakt wirklich etc.)
- Der Faktor soll im Abgleich mit der Ballingformel zuverlässige Werte für ABV(Vol.-%) liefern (max. +/- 0,1 Vol.-%)
- Der Faktor soll für eine möglichst weite Spanne im Bereich Stammwürze und Vergärungsgrad gültig sein
- Der Faktor soll nicht nur für das Endprodukt, sondern für den gesamten Gärverlauf gültig sein (stetige Änderung des Vergärungsgrades)
- Der Faktor sollte seinen "best fit" innerhalb der meistgebrauten Stammwürzeklassen und Vergärungsgrade haben, aber auch darüber und darunter noch mit sehr guter Näherung arbeiten
- Der Faktor sollte auch im Umfeld einer "Übervergärung" zuverlässige Werte liefern (Vergärungsgrad scheinbar Vs bis 100 %)
- Der Faktor sollte unabhängig vom Bierstil, vom Rohstoff, vom Verfahren und vom Hefestamm verlässliche Werte liefern
Kernziel des Faktors ist die einfache Anwendung auf bereits bekannte Größen oder besser: mit möglichst wenig möglichst viel erreichen.
Mit der Stammwürze P [%mas] und dem scheinbaren Restextrakt Es [%mas] sind die bekannten Größen gemeint und für den Faktor ist bekannt, dass er irgendwo zwischen 1,80 - 2,00 liegen muß.
Jetzt war es an der Zeit Beispiele aufzubauen, um genau diesen Faktor zu finden, der die oben aufgeführten Ziele erfüllt.
Vorbereitung der Testumgebung - die Ballingformel
Die Kontrolle des Faktors soll im Abgleich mit der Ballingformel stattfinden. Die Ballingformel kennt aber nur die Parameter
- Stammwürze P in g/100g
- Extrakt wirklich Ew in g/100g
- Alkoholkonzentration Alc. in g/100g
Um aus den bekannten Größen P und Es via Ballingformel direkt eine Alkoholkonzentration in Volumenprozent(ABV) zu berechnen, musste eine Anpassung der Formel her die zusätzlich berücksichtigt:
- die Umrechnung in Ew
- die Dichte von Bier
- die Dichte von Ethanol
- den Massenverlust der Würze auf dem Weg zum Bier durch Hefe und Kohlenstoffdioxid
Die Formel ist recht umfangreich geraten, weshalb hier eine sinnvolle Darstellung kaum möglich ist. Als Alternative dazu gibt es eine Excel-Tabelle zum download mit einem Musterdatensatz und Erklärungen in der Kommentarfunktion. Gerne auch zum prüfen eigener Werte und zum spielen mit geänderten Faktoren zur Berechnung einer resultierenden Alkoholkonzentration. Am Ende des Artikels findet sich ein Downloadbereich, der den Link zur Excel-Tabelle ein weiteres mal veräussert.
Musterdaten für den Vergleich zur Ballingformel
Mit dem in der Tabellenkalkulation bereit gestellten Formelwerk war es keine große Sache mehr, sich beliebig viele Beispiele für die unterschiedlichsten Stammwürzen, Restextraktgehalte - nebst zugehörigen Vergärungsgraden, zu erzeugen.
Im Umgang mit den Beispieldatensätzen hat sich aber gezeigt, dass die Erfassung der Kombination aus P und Es wesentlich mehr Aufwand bedeutet als die Erfassung von P und Vs, weswegen auf der Erfassungsseite P und Vs verwendet wird und der Es ein berechneter Wert ist.
Typischerweise denkt und spricht der Brauer auch so: "Ich habe eine Stammwürze von 12,0 °P und einen Vergärungsgrad von 78,5 %. Mit wieviel Vol.-% muss ich rechnen?"
Ergebnisse
Nach einigem probieren hat sich der Faktor 1,86 für die formulierten Ziele als sehr robust erwiesen. Hier ein Beispiel dafür, wie sich der Faktor 1,86 für die unterschiedlichsten Stammwürzen und Vergärungsgrade im Abgleich mit der Ballingformel verhält (Tabelle 01):
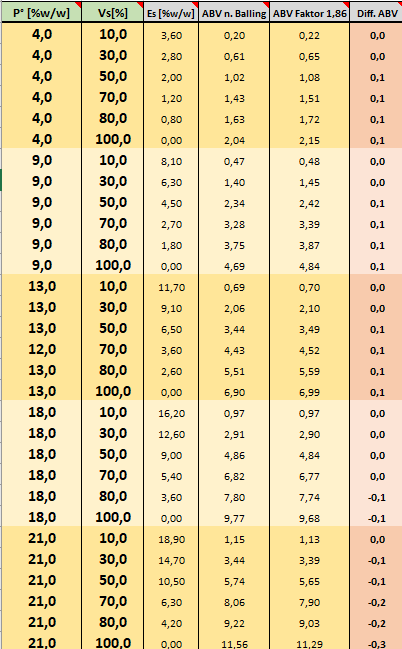
Statistisch ergibt sich für den Faktor 1,86 eine Standardabweichung s zur Ballingformel und für den Wertebereich P = 1 - 21 % und für Vs = 1 - 100 % zu 0,1.
Anton Paar, namentlich Gebhard Sauseng, war noch so freundlich hat mir zur weiteren Überprüfung der Ergebnisse 100 echte Bieranalysen quer durch die Bierstile zur Verfügung gestellt. Aus Datenschutzgründen darf ich diese Bieranalysen hier nicht publizieren, aber die Rechenergebnisse auf Basis echter Daten waren von vergleichbarer Qualität wie die in Tabelle 01.
Zeit, den Faktor festzulegen.
Der neue Faktor, die neue Formel
ABV [Vol.-%] = ( P - Es ) / 1,86
Gültigkeitsbereiche:
- Stammwürze P = 0 % - 21 %
- Vergärungsgrad scheinbar Vs = 0 % - 100 %
- Abweichung Vol.-% zur Ballingformel: +/- 0,1 Vol.-%
Formelzeichen
- ABV: Alcohol by volumne, z.B. ml/100 ml
- Vol.-%: Volumenprozent Alkohol. Identisch mit ABV
- %v/v: Volumen-/Volumenprozent, z.B. ml/100 ml
- ABW: Alcohol by weight, z.B. g/100 g
- %w/w: Gewichts-/Gewichtsprozent, %mas oder GG%, z.B. g/100 g
- P/°P/P%: Stammwürze oder Grad Plato °P in Massen- oder Gewichtsprozent (%mas, %w/w, GG%, g/100g). Im Sprachgebrauch festgelegt als Extraktkonzentration unmittelbar vor der Vergärung und per Definition hat 1 °P dieselbe Massendichte wie eine wässrige Saccharose-Lösung mit einem Gewichtsprozent Saccharose [1g/100g]
- Es%: Extrakt scheinbar in %w/w. Der durch den Alkoholgehalt einer Probe verfälschte Dichtewert für die wirkliche Extraktmenge Ew%. Klassisch der "Spindelwert".
- Ew%: Extrakt wirklich in %w/w. Der Dichtewert für eine Extraktkonzentration ohne den Einfluss des Alkoholgehalts
- Vs%: Vergärungsgrad scheinbar in %. Ein berechneter Wert aus P und Es
- Vw%: Vergärungsgrad wirklich in %. Ein berechneter Wert aus P und Ew
- vEs%: Bereits vergorener scheinbarer Extrakt in %, z.B. vEs% = P - Es%
- vEw%: Bereits vergorener wirklicher Extrakt in %, z.B. vEw% = P - Ew%
- [Q001] Brauer, J.; Lenzini, J.: Vergärungsziffer zur Quantifizierung der Drinkability, BRAUWELT 9-10, 2021, S. 228-232, Fachverlag Hans Carl Nürnberg
- [Q002] Balling, Carl Joseph Napoleon: Die Gährungschemie wissenschaftlich begründet und in ihrer Anwendung auf die Bierbrauerei, Branntweinbrennerei, Hefenerzeugung, Weinbereitung und Essigfabrikation practisch dargestellt, Band 1, Band 2 und Band 3, Verlag F. Tempsky, Prag 1845
- [Q003] Gossett, J. M.: Stoichiometry of Maltose Fermentation to Ethanol, 2012; http://www.ithacoin.com/brewing/stoichiometry.htm
- [Q004] Cutaia, A. J.; Reid, A-J.; Speers, R. A.: Examination of the relationships between original, real, and apparent extracts, and alcohol in pilot plant and commercially produced beers, Journal of the Institute of Brewing, 115 (4), 2009, S. 318–327.; https://onlinelibrary.wiley.com/doi/pdf/10.1002/j.2050-0416.2009.tb00387.x
- Formeln in Excel mit Beispieldatensatz: ABV_BallingFormelUndFaktorImVergleich
- https://www.brewersfriend.com/abv-calculator/
- https://www.brewersfriend.com/2011/06/16/alcohol-by-volume-calculator-updated/
- https://www.brewersfriend.com/refractometer-calculator
- https://www.omnicalculator.com/food/alcohol-by-volume#calculating-abv-from-specific-gravity
- http://www.brewmorebeer.com/calculate-percent-alcohol-in-beer/
- http://www.ithacoin.com/brewing/brewing_calcs/ABV_calc.htm
- http://www.ithacoin.com/brewing/ABV_calc_frontpage.htm
- https://www.gradplato.com/kategorien/know-how/berechnungen-rund-ums-bier
Titelbild: Hankwang at English Wikipedia, Saccharometer, Ausschnitt, CC BY-SA 3.0

